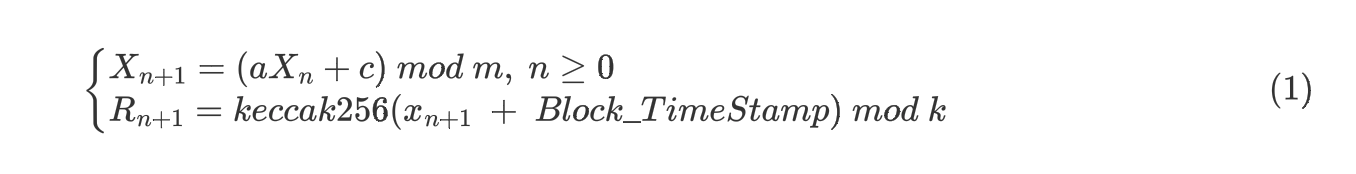基于DGHV的同态加密

基本概念、学习笔记、参考内容：

概念、个人笔记：

1. 同态加密的原理详解与go实践
2. DGHV:整数上的同态加密(1)-算法构建
3. DGHV:整数上的同态加密(2)-解决噪声与构建全同态蓝图

参考：

1. 论文：《一种基于智能合约的全同态加密方法》
2. [1] M. Dijk, C. Gentry, S. Halevi, and V.Vaikuntanathan. Fully homomorphic encryption over the integers[J]. Applications of Cryptographic Techniques: Springer, Berlin, 2010, 24-43.
3. http://blog.sciencenet.cn/blog-411071-617182.html

同态加密等计算量大的算法不适合在合约中计算，合约仅作为测试

本项目代码地址: https://github.com/xwjahahahaha/DGHV

基本设计

1. 随机数

我们所说的随机函数都是伪随机函数即PRF

随机函数的一般构成是：随机种子 + 随机数生成算法

目前有很多优秀的伪随机算法已经实现，但是在区块链智能合约上的最大困难是区块链的封闭性

可以将区块链看作一个封闭式的信息世界，所以不像一般网络中有丰富的熵增源.

Solidity通常采用keccak256哈希函数 作为随机数的生成器，该函数有一定的随机数性质，但是随机数生成的过程容易被攻击。

传统的随机数生成过程需要本结点的 Nonce值作为随机数种子，恶意节点会大量计算Nonce的值，直到随机事件的结果对自己有利，所以项目采用区块时间戳作为随机种子。

使用线性求余法生成随机数，再采用keccak256 Hash函数将区块时间戳与随机数合并取最终的随机数

生成公式如下：

2. 整数上的全同态加密

功能测试

合约实现了输入为单Bit（即m ∈ {0, 1}）的加法同态加密（使用对称秘钥）

step_1 选择参数

编译、运行syn_DGHV.go

对于参数η，加法同态始终满足，但是乘法同态满足有要求（因为算法噪音）：

• 经测试η>=9时，乘法同态满足（小于9时不稳定，可见评估结果输出）
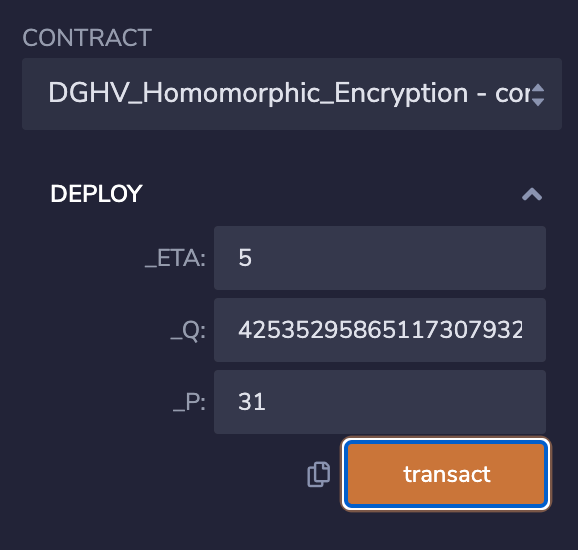
• 智能合约中3<=η<=5, 因为η过大会导致参数q过大无法部署合约（solidity最大为int256，没有大数操作）

go build -o dghv.exe ./ && chmod +x dghv.exe
./dghv.exe 5		# 参数1：η （建议>=9, 合约中<=5）

运行结果中包含：

• 生成的秘钥p
• 参数q

输出示例（输出包含了多组测试，选择一组参数即可）：

==============================================
p =  31
q = 42535295865117307932921825928971026418
m0 = 0, m1 = 1
解密结果：n0 = 0, n1 = 1
加法测试：0 + 1 , true
加法测试：0 + 0 , true
加法测试：1 + 1 , true
加法测试：1 + 0 , true
==============================================
乘法测试：0 * 1 , true
乘法测试：0 * 0 , true
乘法测试：1 * 1 , true
乘法测试：1 * 0 , true
==============================================

step_2 部署合约，输入参数

以remix IDE为例

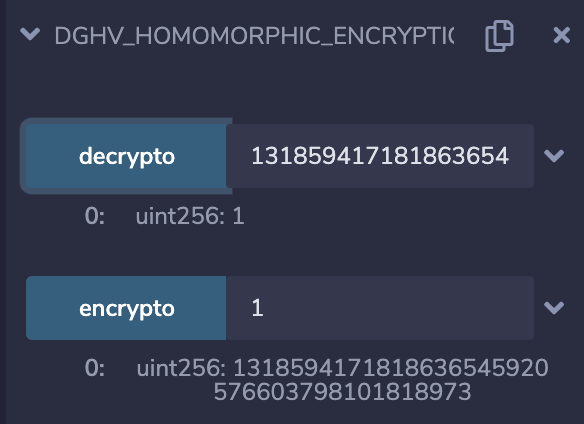
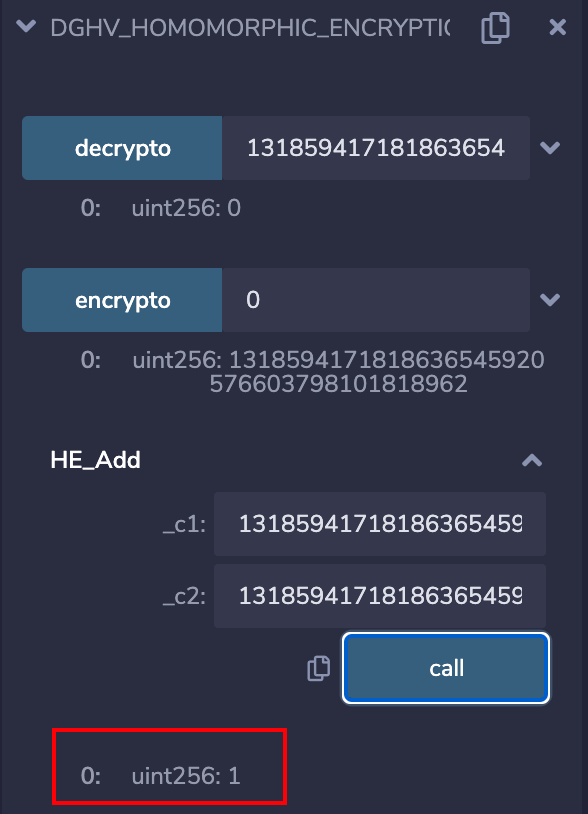
输出初始化参数：

step_3 测试

1的密文为：1318594171818636545920576603798101818973

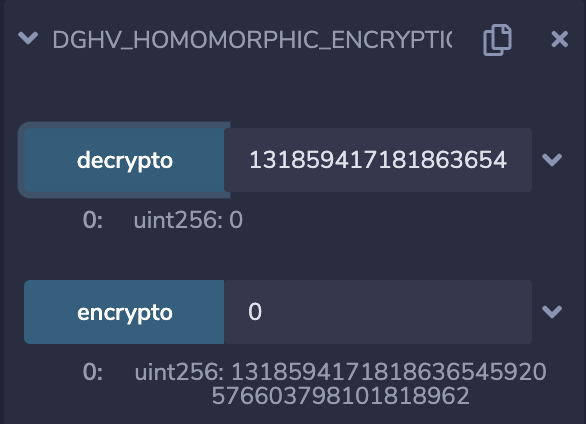
0的密文为：1318594171818636545920576603798101818962

同态加法

1+0 = 1

1+1 = 0

0+0 = 0

拓展与改进

1. 在合约中实现字符串大数的基本计算就可以实现合约上的同态乘法（或许有更好的办法）

2. 虽然输入只支持1bit，但是可以通过组合电路实现高阶的计算：

   • 同态加法 等价于 逻辑异或
   • 同态乘法 等价于 逻辑与
   • 逻辑与与逻辑异或具有完备性，可以实现组合电路任意高阶计算

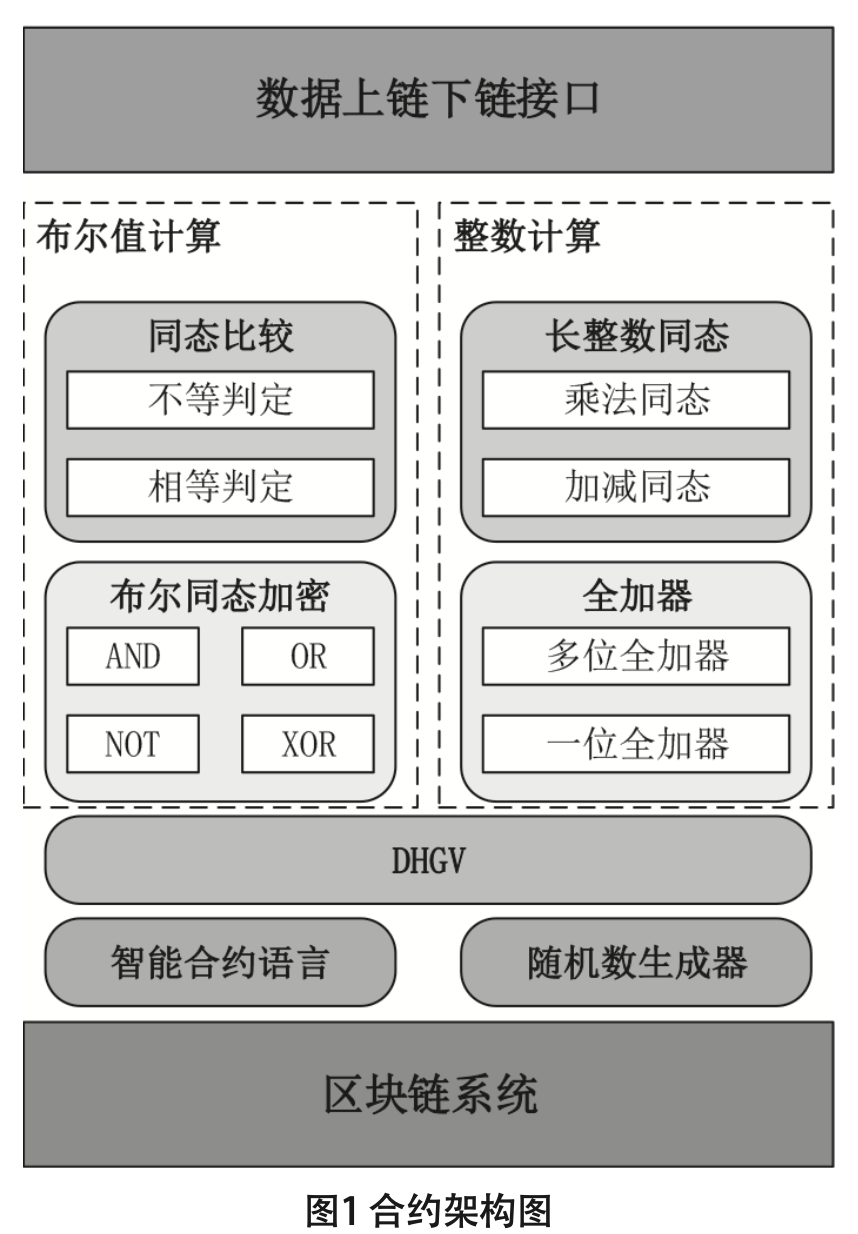
   （图片来自论文）

   

3. 设计电路时注意使用Bootstappable算法减少噪声，不然会失效

欢迎Start，后续继续更新