本项目包含 LeetCode、《剑指 Offer(第 2 版)》、《剑指 Offer(专项突击版)》、《程序员面试金典(第 6 版)》等题目的相关题解。所有题解均由多种编程语言实现,包括但不限于:Java、Python、C++、JavaScript、C#、Go,日常更新。欢迎 Star 🌟 关注本项目,获取项目最新动态。
- Gitee Pages: https://doocs.gitee.io/leetcode
- GitHub Pages: https://doocs.github.io/leetcode
- 在排序数组中查找元素的第一个和最后一个位置 - 二分查找
- 准时到达的列车最小时速 - 二分查找
- 找到需要补充粉笔的学生编号 - 二分查找
- 可移除字符的最大数目 - 二分查找
- 图像渲染- BFS、DFS、Flood Fill 算法、连通性模型
- 岛屿数量 - BFS、Flood Fill 算法
- 01 矩阵 - 多源 BFS
- 地图中的最高点 - 多源 BFS
- 进击的骑士 - BFS、最短路模型
- 二进制矩阵中的最短路径 - BFS、最短路模型
- 迷宫中离入口最近的出口 - BFS、最短路模型
- 网格中的最短路径 - BFS、最短路模型
- 打开转盘锁 - 最小步数模型、双向 BFS、A* 算法
- 单词接龙 - 最小步数模型、双向 BFS
- 转化数字的最小运算数 - 最小步数模型、双向 BFS
- 滑动谜题 - BFS、最小步数模型、A* 算法
- 访问所有节点的最短路径 - BFS、最小步数模型、A* 算法
- 为高尔夫比赛砍树 - BFS、A* 算法
- 使网格图至少有一条有效路径的最小代价 - 双端队列 BFS
- 迷宫 - DFS、连通性模型、Flood Fill 算法
- 单词搜索 - DFS、搜索顺序、回溯
- 黄金矿工 - DFS、搜索顺序、回溯
- 杨辉三角 - 线性 DP、数字三角形模型
- 最小路径和 - 线性 DP、数字三角形模型
- 摘樱桃 - 线性 DP、数字三角形模型
- 摘樱桃 II - 线性 DP、数字三角形模型
- 最长递增子序列 - 线性 DP、最长上升子序列模型
- 删列造序 III - 线性 DP、最长上升子序列模型
- 俄罗斯套娃信封问题 - 线性 DP、最长上升子序列模型、贪心优化
- 二维网格图中探测环 - 并查集、检测环
- 除法求值 - 并查集、权值维护
- 由斜杠划分区域 - 并查集、连通分量个数
- 水位上升的泳池中游泳 - 并查集
- 交换字符串中的元素 - 并查集
- 打砖块 - 并查集、逆向思维
- 尽量减少恶意软件的传播 II - 并查集、逆向思维
- 检查边长度限制的路径是否存在 - 并查集、离线思维
- 保证图可完全遍历 - 双并查集
- 区域和检索 - 数组可修改 - 树状数组、线段树
- 通过指令创建有序数组 - 树状数组、线段树
- 统计数组中好三元组数目 - 树状数组、线段树
- 最多 K 次交换相邻数位后得到的最小整数 - 树状数组
- 二维区域和检索 - 可变 - 二维树状数组、线段树
- 计算右侧小于当前元素的个数 - 离散化树状数组、线段树
- 区间和的个数 - 离散化树状数组、线段树
- 翻转对 - 离散化树状数组、分治归并、线段树
- 最长递增子序列的个数 - 离散化树状数组、区间最值问题
- 奇妙序列 - 动态开点线段树、懒标记
- Range 模块 - 动态开点线段树、懒标记
- 我的日程安排表 III - 动态开点线段树、懒标记
- 每天绘制的新区域数量 - 动态开点线段树、懒标记、区间染色模型
- 由单个字符重复的最长子字符串 - 线段树、动态最大子段和模型
- 矩形面积 II - 线段树、离散化、扫描线
刷编程题的最大好处就是可以锻炼解决问题的思维能力。相信我,「如何去思考」 本身也是一项需要不断学习和练习的技能。非常感谢前微软工程师、现蚂蚁金服技术专家 @kfstorm 贡献了本项目的所有 C# 题解。
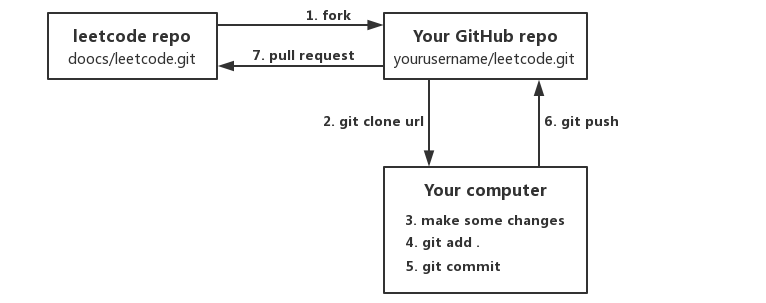
如果你对本项目感兴趣,并且希望加入我们刷题小分队,欢迎随时提交 PR。请参考如下步骤:
- 将本项目 fork 到你的个人 GitHub 帐户,然后 clone 到你的本地机器;
- 对项目做出一些变更,然后使用 git add、commit、push 等命令将你的本地变更提交到你的远程 GitHub 仓库;
- 将你的变更以 PR 的形式提交过来,项目的维护人员会在第一时间对你的变更进行 review!
- 你也可以参考帮助文档 https://help.github.com/cn 了解更多细节。
Gitpod.io 是一个免费的在线开发环境,你也可以使用它参与本项目。
感谢以下所有朋友对本项目的贡献!
感谢以下个人、组织对本项目的支持和赞助!
"You help the developer community practice for interviews, and there is nothing better we could ask for." -- Alan Yessenbayev
知名互联网科技博主 @爱可可-爱生活 微博推荐。