Single-box-conv network (from `test-mnist.py`) learns patterns on MNIST
This is a PyTorch implementation of the box convolution layer as introduced in the 2018 NeurIPS paper:
Burkov, E., & Lempitsky, V. (2018) Deep Neural Networks with Box Convolutions. Advances in Neural Information Processing Systems 31, 6214-6224.
git clone https://github.com/shrubb/box-convolutions.git && cd box-convolutions
pip3 install --user .
python3 -m box_convolution.test # if throws errors, please open a GitHub issueTo uninstall:
pip3 uninstall box_convolutionimport torch
from box_convolution import BoxConv2d
box_conv = BoxConv2d(16, 8, 240, 320)
help(BoxConv2d)Also, there is a usage example in test-mnist.py.
Tested on Ubuntu 18.04.2, Python 3.6, PyTorch 1.0.0, GCC 7.3.0, CUDA 9.2. Other versions (e.g. Python 2.7 or PyTorch 0.4 or GCC 5 or CUDA 8 or CUDA 10) should work too, but I haven't checked. If something doesn't build, please open an issue.
CUDA 9/9.1 + GCC 6 isn't supported, see this issue.
You may want to see our poster.
3×3 convolutions are too small ⮕ receptive field grows too slow ⮕ ConvNets have to be very deep.
This is especially undesirable in dense prediction tasks (segmentation, depth estimation, object detection, ...).
Today people solve this by
- dilated/deformable convolutions (can bring artifacts or degrade to
1×1conv; almost always filter high-frequency); - "global" spatial pooling layers (usually too constrained, fixed size, not "fully convolutional").
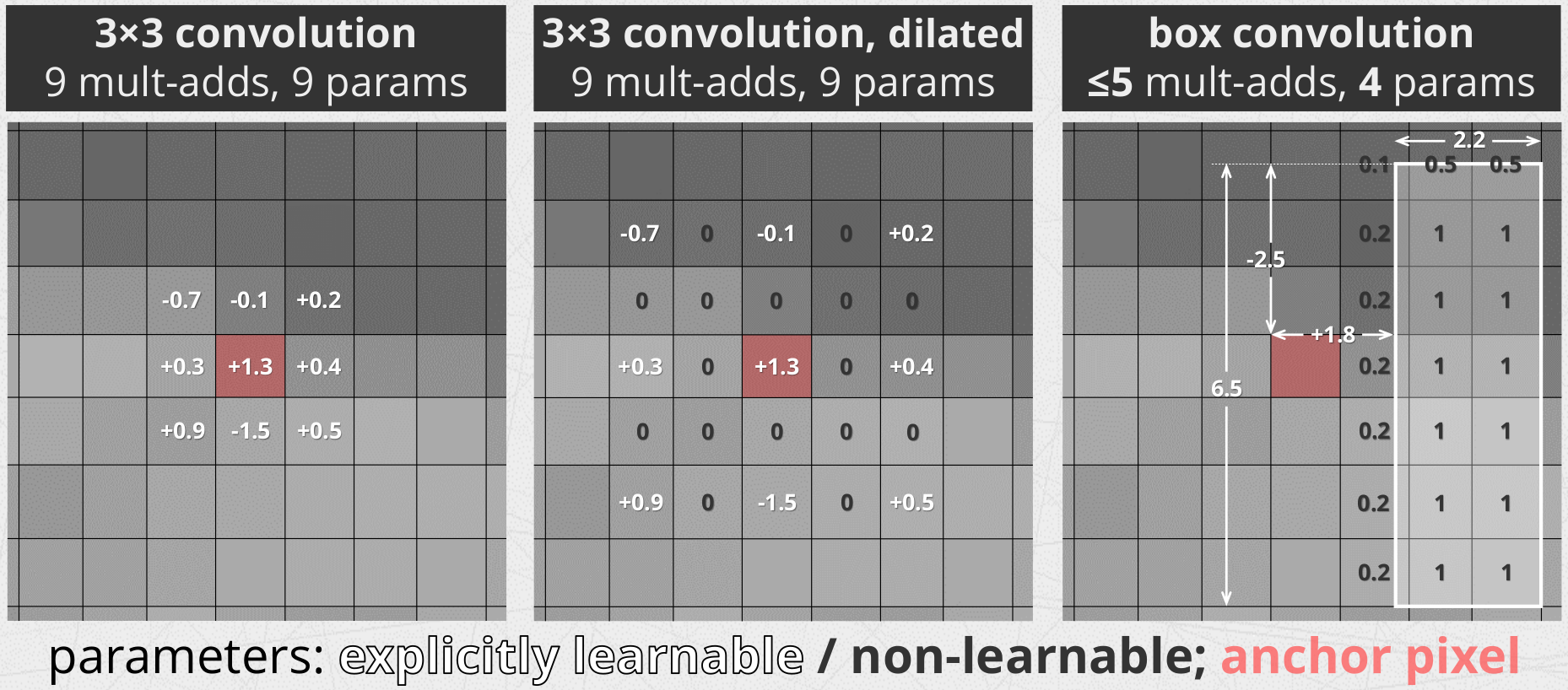
Box convolution layer is a basic depthwise convolution (i.e. Conv2d with groups=in_channels) but with special kernels called box kernels.
A box kernel is a rectangular averaging filter. That is, filter values are fixed and unit! Instead, we learn four parameters per rectangle − its size and offset:
One example: there is an efficient semantic segmentation model ENet. It's a classical hourglass architecture stacked of dozens ResNet-like blocks (left image).
Let's replace some of these blocks by our "box convolution block" (right image).
First we replaced every second block with a box convolution block (BoxENet in the paper). The model became
- more accurate,
- faster,
- lighter
- without dilated convolutions.
Then, we replaced every residual block (except the down- and up-sampling ones)! The result, BoxOnlyENet, is
- a ConvNet almost without (traditional learnable weight) convolutions,
- 2 times less operations,
- 3 times less parameters,
- still more accurate than ENet!