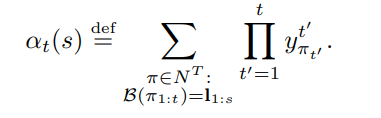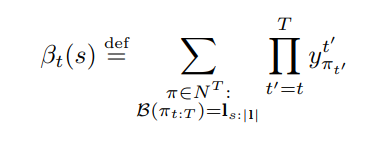This is an implementation in Numpy of the CTC loss (https://www.cs.toronto.edu/~graves/icml_2006.pdf).
The CTC (Connectionist Temporal Classification) is commonly used in sequence to sequence modelling such as OCR or ASR, and has the great benefit of not requiring time-specific GT labeling.
Define an Alphabet of size |L|, e.g. L = {a, b, c, ..., z} and add a special token called the blank token "-", which gives the full alphabet L'={a, b, c, ..., z, -}.
Given a model which outputs a tensor of size (T, |L'|), we treat it as a character prediction per timestep. If we take the maximum score in each timestep, we get a naive (typically called "argmax") assessment of what the model predicted. Supported by this loss, the model is given great freedom in choosing where to place each character. The prediction "---h--i" is in a sense equal to the prediction "h----i-", since both predictions "collapse" into the same string: "hi".
The exact functionality of "collapse" (called B in the original paper), is: "simply removing all blanks and repeated labels ... (e.g. B("a−ab−") = B("−aa−−abb") = aab)"
This is useful during inference, but during training, what's the methodology? We notice that many paths lead to the same label. For an output of 3 timesteps, the label "hi" can be reached by 5 paths: "hi-", "h-i", "-hi", "hhi", "hii". Typically we have hundreds of timesteps, so there are much more possible paths.
In principle, we wish to maximize the probability of the label, treating the matrix as a probability distribution over the alphabet L' in each timestep. To do so, we sum over all paths in the matrix which collapse into the gt label:
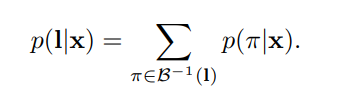
In order to calculate this expression, and to derive gradients from it, the paper employs a forwards-backwards algorithm which is implemented in this repository. Specifically, two matrices Alpha and Beta are calculated with dynamic programming:
After doing so, we can calculate P(l|x) and the gradients for x - see formulas 14 & 15 in the original paper.
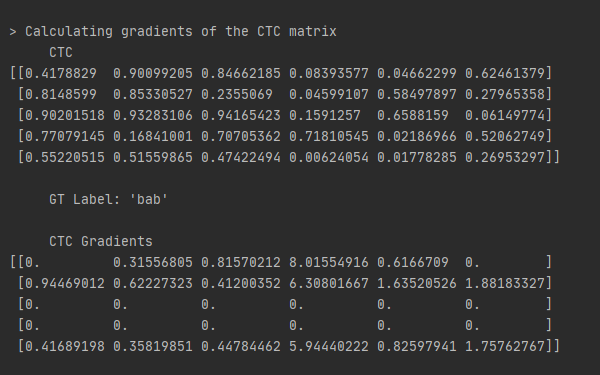
In the code we generate a random matrix of size (T, L'), as if it were an output of a sequence-to-sequence model, then we calculate its gradients using the forward-backward algorithm.
As can be seen, gradients exist only in the two top rows which correspond to 'a' and 'b', as well as the last row which corresponds to '-'. This makes sense, since we maximize P(l|x), which means we only punish in rows which valid paths (which collapse into the gt label) go through.
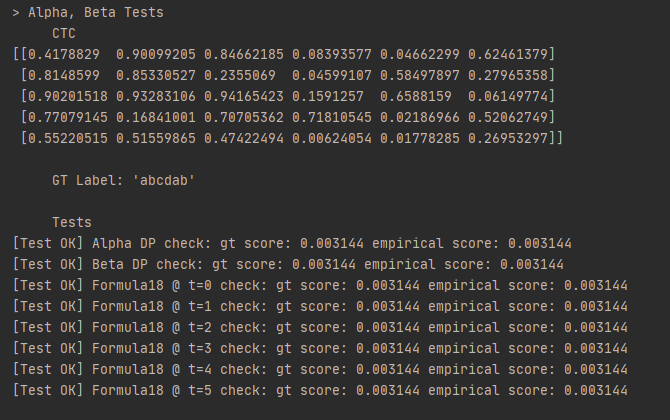
Further, a test for the Alpha, Beta matrices is added, to verify by experiment - mostly for myself - that formula 18 from the paper as well as my own implementation works:
Enjoy!