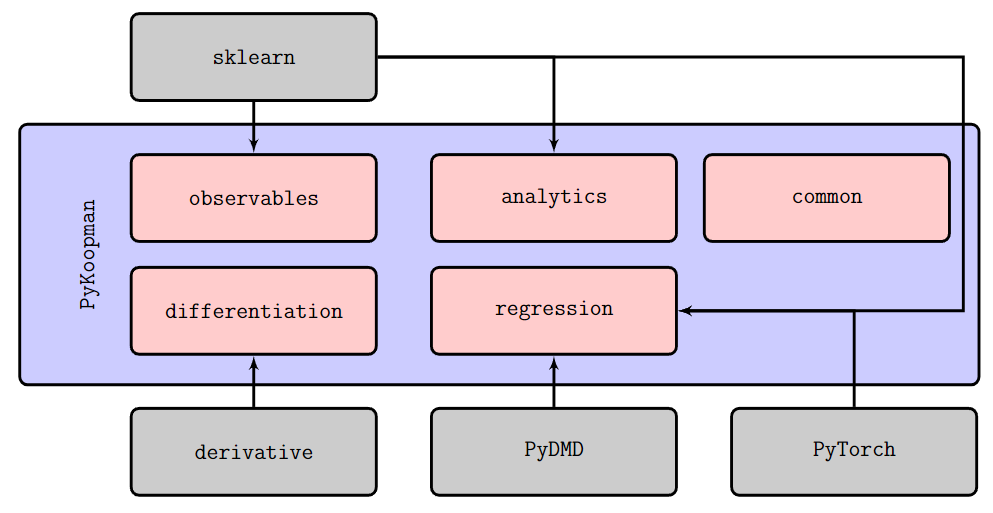
PyKoopman is a Python package for computing data-driven approximations to the Koopman operator.
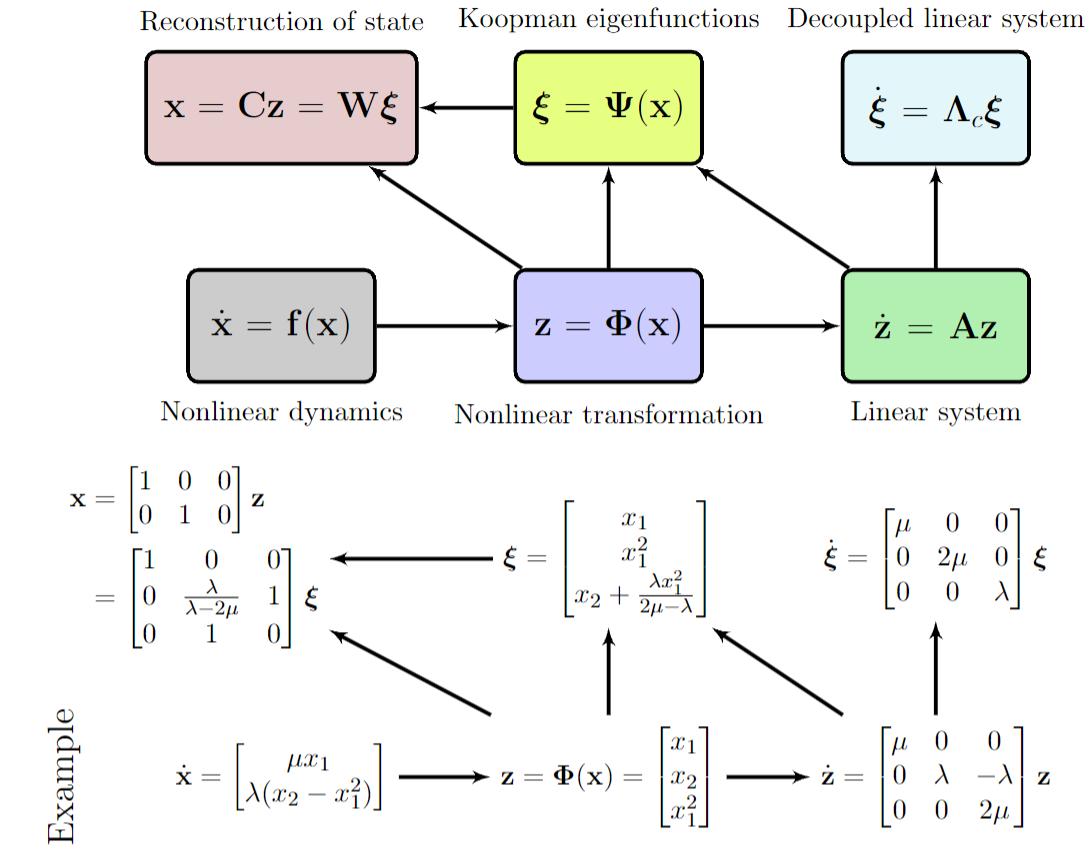
Given a nonlinear dynamical system,
x'(t) = f(x(t)),
the Koopman operator governs the temporal evolution of the measurement function. Unfortunately, it is an infinite-dimensional linear operator. Most of the time, one has to project the Koopman operator onto a finite-dimensional subspace that is spanned by user-defined/data-adaptive functions.
z = \Phi(x).
If the system state is also contained in such subspace, then effectively, the nonlinear dynamical system is (approximately) linearized in a global sense.
The goal of data-driven approximation of Koopman operator is to find such a set of functions that span such lifted space and the transition matrix associated with the lifted system.
PyKoopman package is centered around the Koopman class and KoopmanContinuous class. It consists of two key components
observables: a set of observables functions, which spans the subspace for projection.regressor: the optimization algorithm to find the bestfitfor the projection of Koopman operator.
After Koopman/KoopmanContinuous object has been created, it must be fit to data, similar to a scikit-learn model.
We design PyKoopman such that it is compatible to scikit-learn objects and methods as much as possible.
- Observable library for lifting the state into the observable space
- Identity (for DMD/DMDc or in case users want to compute observables themselves):
Identity - Multivariate polynomials:
Polynomial - Time delay coordinates:
TimeDelay - Radial basis functions:
RadialBasisFunctions - Random Fourier features:
RandomFourierFeatures - Custom library (defined by user-supplied functions):
CustomObservables - Concatenation of observables:
ConcatObservables
- Identity (for DMD/DMDc or in case users want to compute observables themselves):
- System identification method for performing regression
- Dynamic mode decomposition:
PyDMDRegressor - Dynamic mode decomposition with control:
DMDc - Extended dynamic mode decomposition:
EDMD - Extended dynamic mode decomposition with control:
EDMDc - Kernel dynamic mode decomposition:
KDMD - Hankel Alternative View of Koopman Analysis:
HAVOK - Neural Network DMD:
NNDMD
- Dynamic mode decomposition:
- Sparse construction of Koopman invariant subspace
- Multi-task learning based on linearity consistency
- Learning how to create observables
- Learning how to compute time derivatives
- Dynamic mode decomposition on two mixed spatial signals
- Dynamic mode decomposition with control on a 2D linear system
- Dynamic mode decomposition with control (DMDc) for a 128D system
- Dynamic mode decomposition with control on a high-dimensional linear system
- Successful examples of using Dynamic mode decomposition on PDE system
- Unsuccessful examples of using Dynamic mode decomposition on PDE system
- Extended DMD for Van Der Pol System
- Learning Koopman eigenfunctions on Slow manifold
- Comparing DMD and KDMD for Slow manifold dynamics
- Extended DMD with control for chaotic duffing oscillator
- Extended DMD with control for Van der Pol oscillator
- Hankel Alternative View of Koopman Operator for Lorenz System
- Hankel DMD with control for Van der Pol Oscillator
- Neural Network DMD on Slow Manifold
- EDMD and NNDMD for a simple linear system
- Sparisfying a minimal Koopman invariant subspace from EDMD for a simple linear system
- Python == 3.10
If you are using Linux or macOS you can install PyKoopman with pip:
pip install pykoopmanFirst clone this repository:
git clone https://github.com/dynamicslab/pykoopmanSecond, it is highly recommended to use venv to get a local python environment
python -m venv venv
source ./venv/bin/activateIn windows, you activate virtual environment in a different way
.\venv\Scripts\activate.ps1Then, to install the package, run
python -m pip install -e .If you do not have root access, you should add the --user option to the above lines.
After you download the Github package, go to the directory, type
python -m pip install -r requirements-dev.txtThe documentation for PyKoopman is hosted on Read the Docs.
We welcome contributions to PyKoopman. To contribute a new feature please submit a pull request. To get started we recommend installing the packages in "developer mode" via
python -m pip install -e .[dev]This will allow you to run unit tests and automatically format your code. To be accepted your code should conform to PEP8 and pass all unit tests. Code can be tested by invoking
pytestWe recommed using pre-commit to format your code. Once you have staged changes to commit
git add path/to/changed/file.pyyou can run the following to automatically reformat your staged code
pre-commit -a -vNote that you will then need to re-stage any changes pre-commit made to your code.
If you find a bug in the code or want to request a new feature, please open an issue.
Known issues:
- Python 3.12 might cause unexpected problems.
@article{Pan2024, doi = {10.21105/joss.05881},
url = {https://doi.org/10.21105/joss.05881},
year = {2024},
publisher = {The Open Journal},
volume = {9},
number = {94},
pages = {5881},
author = {Shaowu Pan and Eurika Kaiser and Brian M. de Silva and J. Nathan Kutz and Steven L. Brunton},
title = {PyKoopman: A Python Package for Data-Driven Approximation of the Koopman Operator},
journal = {Journal of Open Source Software}}
- PySINDy - A Python libray for the Sparse Identification of Nonlinear Dynamical systems (SINDy) method introduced in Brunton et al. (2016a).
- Deeptime - A Python library for the analysis of time series data with methods for dimension reduction, clustering, and Markov model estimation.
- PyDMD - A Python package using the Dynamic Mode Decomposition (DMD) for a data-driven model simplification based on spatiotemporal coherent structures. DMD is a great alternative to SINDy.
- pykoop - a Koopman operator identification library written in Python
- DLKoopman - a deep learning library for Koopman operator