This is a Recurrent Neural Network library that extends Torch's nn. You can use it to build RNNs, LSTMs, GRUs, BRNNs, BLSTMs, and so forth and so on. This library includes documentation for the following objects:
Modules that consider successive calls to forward as different time-steps in a sequence :
- AbstractRecurrent : an abstract class inherited by Recurrent and LSTM;
- Recurrent : a generalized recurrent neural network container;
- LSTM : a vanilla Long-Short Term Memory module;
- FastLSTM : a faster LSTM with optional support for batch normalization;
- GRU : Gated Recurrent Units module;
- MuFuRu : Multi-function Recurrent Unit module;
- Recursor : decorates a module to make it conform to the AbstractRecurrent interface;
- Recurrence : decorates a module that outputs
output(t)given{input(t), output(t-1)}; - NormStabilizer : implements norm-stabilization criterion (add this module between RNNs);
Modules that forward entire sequences through a decorated AbstractRecurrent instance :
- AbstractSequencer : an abstract class inherited by Sequencer, Repeater, RecurrentAttention, etc.;
- Sequencer : applies an encapsulated module to all elements in an input sequence (Tensor or Table);
- SeqLSTM : a very fast version of
nn.Sequencer(nn.FastLSTM)where theinputandoutputare tensors; - SeqLSTMP :
SeqLSTMwith a projection layer; - SeqGRU : a very fast version of
nn.Sequencer(nn.GRU)where theinputandoutputare tensors; - SeqBRNN : Bidirectional RNN based on SeqLSTM;
- BiSequencer : used for implementing Bidirectional RNNs and LSTMs;
- BiSequencerLM : used for implementing Bidirectional RNNs and LSTMs for language models;
- Repeater : repeatedly applies the same input to an AbstractRecurrent instance;
- RecurrentAttention : a generalized attention model for REINFORCE modules;
Miscellaneous modules and criterions :
- MaskZero : zeroes the
outputandgradOutputrows of the decorated module for commensurateinputrows which are tensors of zeros; - TrimZero : same behavior as
MaskZero, but more efficient wheninputcontains lots zero-masked rows; - LookupTableMaskZero : extends
nn.LookupTableto support zero indexes for padding. Zero indexes are forwarded as tensors of zeros; - MaskZeroCriterion : zeros the
gradInputanderrrows of the decorated criterion for commensurateinputrows which are tensors of zeros; - SeqReverseSequence : reverses an input sequence on a specific dimension;
Criterions used for handling sequential inputs and targets :
- SequencerCriterion : sequentially applies the same criterion to a sequence of inputs and targets (Tensor or Table).
- RepeaterCriterion : repeatedly applies the same criterion with the same target on a sequence.
The following are example training scripts using this package :
- RNN/LSTM/GRU for Penn Tree Bank dataset;
- Noise Contrastive Estimate for training multi-layer SeqLSTM language models on the Google Billion Words dataset. The example uses MaskZero to train independent variable length sequences using the NCEModule and NCECriterion. This script is our fastest yet boasting speeds of 20,000 words/second (on NVIDIA Titan X) with a 2-layer LSTM having 250 hidden units, a batchsize of 128 and sequence length of a 100. Note that you will need to have Torch installed with Lua instead of LuaJIT;
- Recurrent Model for Visual Attention for the MNIST dataset;
- Encoder-Decoder LSTM shows you how to couple encoder and decoder
LSTMsfor sequence-to-sequence networks; - Simple Recurrent Network shows a simple example for building and training a simple recurrent neural network;
- Simple Sequencer Network is a version of the above script that uses the Sequencer to decorate the
rnninstead; - Sequence to One demonstrates how to do many to one sequence learning as is the case for sentiment analysis;
- Multivariate Time Series demonstrates how train a simple RNN to do multi-variate time-series predication.
- rnn-benchmarks : benchmarks comparing Torch (using this library), Theano and TensorFlow.
- Harvard Jupyter Notebook Tutorial : an in-depth tutorial for how to use the Element-Research rnn package by Harvard University;
- dpnn : this is a dependency of the rnn package. It contains useful nn extensions, modules and criterions;
- dataload : a collection of torch dataset loaders;
- RNN/LSTM/BRNN/BLSTM training script for Penn Tree Bank or Google Billion Words datasets;
- A brief (1 hours) overview of Torch7, which includes some details about the rnn packages (at the end), is available via this NVIDIA GTC Webinar video. In any case, this presentation gives a nice overview of Logistic Regression, Multi-Layer Perceptrons, Convolutional Neural Networks and Recurrent Neural Networks using Torch7;
- Sequence to Sequence mapping using encoder-decoder RNNs : a complete training example using synthetic data.
- ConvLSTM is a repository for training a Spatio-temporal video autoencoder with differentiable memory.
- An time series example for univariate timeseries prediction.
If you use rnn in your work, we'd really appreciate it if you could cite the following paper:
Léonard, Nicholas, Sagar Waghmare, Yang Wang, and Jin-Hwa Kim. rnn: Recurrent Library for Torch. arXiv preprint arXiv:1511.07889 (2015).
Any significant contributor to the library will also get added as an author to the paper. A significant contributor is anyone who added at least 300 lines of code to the library.
Most issues can be resolved by updating the various dependencies:
luarocks install torch
luarocks install nn
luarocks install dpnn
luarocks install torchxIf you are using CUDA :
luarocks install cutorch
luarocks install cunn
luarocks install cunnxAnd don't forget to update this package :
luarocks install rnnIf that doesn't fix it, open and issue on github.
An abstract class inherited by Recurrent, LSTM and GRU. The constructor takes a single argument :
rnn = nn.AbstractRecurrent([rho])Argument rho is the maximum number of steps to backpropagate through time (BPTT).
Sub-classes can set this to a large number like 99999 (the default) if they want to backpropagate through
the entire sequence whatever its length. Setting lower values of rho are
useful when long sequences are forward propagated, but we only whish to
backpropagate through the last rho steps, which means that the remainder
of the sequence doesn't need to be stored (so no additional cost).
Returns a module for time-step step. This is used internally by sub-classes
to obtain copies of the internal recurrentModule. These copies share
parameters and gradParameters but each have their own output, gradInput
and any other intermediate states.
This is a method reserved for internal use by Recursor
when doing backward propagation. It sets the object's output attribute
to point to the output at time-step step.
This method was introduced to solve a very annoying bug.
Decorates the internal recurrentModule with MaskZero.
The output Tensor (or table thereof) of the recurrentModule
will have each row (i.e. samples) zeroed when the commensurate row of the input
is a tensor of zeros.
The nInputDim argument must specify the number of non-batch dims
in the first Tensor of the input. In the case of an input table,
the first Tensor is the first one encountered when doing a depth-first search.
Calling this method makes it possible to pad sequences with different lengths in the same batch with zero vectors.
When a sample time-step is masked (i.e. input is a row of zeros), then
the hidden state is effectively reset (i.e. forgotten) for the next non-mask time-step.
In other words, it is possible seperate unrelated sequences with a masked element.
Decorates the internal recurrentModule with TrimZero.
Forward propagates the input for the current step. The outputs or intermediate
states of the previous steps are used recurrently. This is transparent to the
caller as the previous outputs and intermediate states are memorized. This
method also increments the step attribute by 1.
Like backward, this method should be called in the reverse order of
forward calls used to propagate a sequence. So for example :
rnn = nn.LSTM(10, 10) -- AbstractRecurrent instance
local outputs = {}
for i=1,nStep do -- forward propagate sequence
outputs[i] = rnn:forward(inputs[i])
end
for i=nStep,1,-1 do -- backward propagate sequence in reverse order
gradInputs[i] = rnn:backward(inputs[i], gradOutputs[i])
end
rnn:forget()The reverse order implements backpropagation through time (BPTT).
Like updateGradInput, but for accumulating gradients w.r.t. parameters.
This method goes hand in hand with forget. It is useful when the current
time-step is greater than rho, at which point it starts recycling
the oldest recurrentModule sharedClones,
such that they can be reused for storing the next step. This offset
is used for modules like nn.Recurrent that use a different module
for the first step. Default offset is 0.
This method brings back all states to the start of the sequence buffers,
i.e. it forgets the current sequence. It also resets the step attribute to 1.
It is highly recommended to call forget after each parameter update.
Otherwise, the previous state will be used to activate the next, which
will often lead to instability. This is caused by the previous state being
the result of now changed parameters. It is also good practice to call
forget at the start of each new sequence.
This method sets the maximum number of time-steps for which to perform
backpropagation through time (BPTT). So say you set this to rho = 3 time-steps,
feed-forward for 4 steps, and then backpropgate, only the last 3 steps will be
used for the backpropagation. If your AbstractRecurrent instance is wrapped
by a Sequencer, this will be handled auto-magically by the Sequencer.
Otherwise, setting this value to a large value (i.e. 9999999), is good for most, if not all, cases.
This method was deprecated Jan 6, 2016.
Since then, by default, AbstractRecurrent instances use the
backwardOnline behaviour.
See updateGradInput for details.
In training mode, the network remembers all previous rho (number of time-steps)
states. This is necessary for BPTT.
During evaluation, since their is no need to perform BPTT at a later time, only the previous step is remembered. This is very efficient memory-wise, such that evaluation can be performed using potentially infinite-length sequence.
References :
- A. Sutsekever Thesis Sec. 2.5 and 2.8
- B. Mikolov Thesis Sec. 3.2 and 3.3
- C. RNN and Backpropagation Guide
A composite Module for implementing Recurrent Neural Networks (RNN), excluding the output layer.
The nn.Recurrent(start, input, feedback, [transfer, rho, merge]) constructor takes 6 arguments:
start: the size of the output (excluding the batch dimension), or a Module that will be inserted between theinputModule andtransfermodule during the first step of the propagation. Whenstartis a size (a number ortorch.LongTensor), then this start Module will be initialized asnn.Add(start)(see Ref. A).input: a Module that processes input Tensors (or Tables). Output must be of same size asstart(or its output in the case of astartModule), and same size as the output of thefeedbackModule.feedback: a Module that feedbacks the previous output Tensor (or Tables) up to themergemodule.merge: a table Module that merges the outputs of theinputandfeedbackModule before being forwarded through thetransferModule.transfer: a non-linear Module used to process the output of themergemodule, or in the case of the first step, the output of thestartModule.rho: the maximum amount of backpropagation steps to take back in time. Limits the number of previous steps kept in memory. Due to the vanishing gradients effect, references A and B recommendrho = 5(or lower). Defaults to 99999.
An RNN is used to process a sequence of inputs.
Each step in the sequence should be propagated by its own forward (and backward),
one input (and gradOutput) at a time.
Each call to forward keeps a log of the intermediate states (the input and many Module.outputs)
and increments the step attribute by 1.
Method backward must be called in reverse order of the sequence of calls to forward in
order to backpropgate through time (BPTT). This reverse order is necessary
to return a gradInput for each call to forward.
The step attribute is only reset to 1 when a call to the forget method is made.
In which case, the Module is ready to process the next sequence (or batch thereof).
Note that the longer the sequence, the more memory that will be required to store all the
output and gradInput states (one for each time step).
To use this module with batches, we suggest using different
sequences of the same size within a batch and calling updateParameters
every rho steps and forget at the end of the sequence.
Note that calling the evaluate method turns off long-term memory;
the RNN will only remember the previous output. This allows the RNN
to handle long sequences without allocating any additional memory.
For a simple concise example of how to make use of this module, please consult the simple-recurrent-network.lua training script.
Note that any AbstractRecurrent instance can be decorated with a Sequencer
such that an entire sequence (a table) can be presented with a single forward/backward call.
This is actually the recommended approach as it allows RNNs to be stacked and makes the
rnn conform to the Module interface, i.e. each call to forward can be
followed by its own immediate call to backward as each input to the
model is an entire sequence, i.e. a table of tensors where each tensor represents
a time-step.
seq = nn.Sequencer(module)The simple-sequencer-network.lua training script
is equivalent to the above mentionned simple-recurrent-network.lua
script, except that it decorates the rnn with a Sequencer which takes
a table of inputs and gradOutputs (the sequence for that batch).
This lets the Sequencer handle the looping over the sequence.
You should only think about using the AbstractRecurrent modules without
a Sequencer if you intend to use it for real-time prediction.
Actually, you can even use an AbstractRecurrent instance decorated by a Sequencer
for real time prediction by calling Sequencer:remember() and presenting each
time-step input as {input}.
Other decorators can be used such as the Repeater or RecurrentAttention.
The Sequencer is only the most common one.
References :
- A. Speech Recognition with Deep Recurrent Neural Networks
- B. Long-Short Term Memory
- C. LSTM: A Search Space Odyssey
- D. nngraph LSTM implementation on github
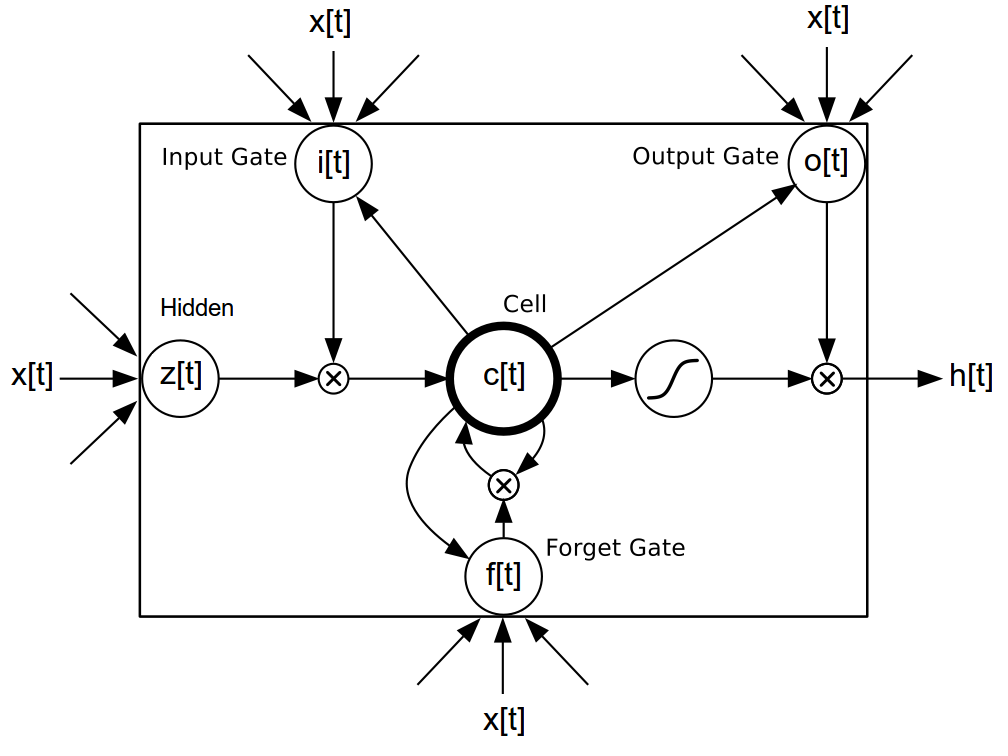
This is an implementation of a vanilla Long-Short Term Memory module. We used Ref. A's LSTM as a blueprint for this module as it was the most concise. Yet it is also the vanilla LSTM described in Ref. C.
The nn.LSTM(inputSize, outputSize, [rho]) constructor takes 3 arguments:
inputSize: a number specifying the size of the input;outputSize: a number specifying the size of the output;rho: the maximum amount of backpropagation steps to take back in time. Limits the number of previous steps kept in memory. Defaults to 9999.
The actual implementation corresponds to the following algorithm:
i[t] = σ(W[x->i]x[t] + W[h->i]h[t−1] + W[c->i]c[t−1] + b[1->i]) (1)
f[t] = σ(W[x->f]x[t] + W[h->f]h[t−1] + W[c->f]c[t−1] + b[1->f]) (2)
z[t] = tanh(W[x->c]x[t] + W[h->c]h[t−1] + b[1->c]) (3)
c[t] = f[t]c[t−1] + i[t]z[t] (4)
o[t] = σ(W[x->o]x[t] + W[h->o]h[t−1] + W[c->o]c[t] + b[1->o]) (5)
h[t] = o[t]tanh(c[t]) (6)where W[s->q] is the weight matrix from s to q, t indexes the time-step,
b[1->q] are the biases leading into q, σ() is Sigmoid, x[t] is the input,
i[t] is the input gate (eq. 1), f[t] is the forget gate (eq. 2),
z[t] is the input to the cell (which we call the hidden) (eq. 3),
c[t] is the cell (eq. 4), o[t] is the output gate (eq. 5),
and h[t] is the output of this module (eq. 6). Also note that the
weight matrices from cell to gate vectors are diagonal W[c->s], where s
is i,f, or o.
As you can see, unlike Recurrent, this implementation isn't generic enough that it can take arbitrary component Module definitions at construction. However, the LSTM module can easily be adapted through inheritance by overriding the different factory methods :
buildGate: builds generic gate that is used to implement the input, forget and output gates;buildInputGate: builds the input gate (eq. 1). Currently callsbuildGate;buildForgetGate: builds the forget gate (eq. 2). Currently callsbuildGate;buildHidden: builds the hidden (eq. 3);buildCell: builds the cell (eq. 4);buildOutputGate: builds the output gate (eq. 5). Currently callsbuildGate;buildModel: builds the actual LSTM model which is used internally (eq. 6).
Note that we recommend decorating the LSTM with a Sequencer
(refer to this for details).
A faster version of the LSTM. Basically, the input, forget and output gates, as well as the hidden state are computed at one fellswoop.
Note that FastLSTM does not use peephole connections between cell and gates. The algorithm from LSTM changes as follows:
i[t] = σ(W[x->i]x[t] + W[h->i]h[t−1] + b[1->i]) (1)
f[t] = σ(W[x->f]x[t] + W[h->f]h[t−1] + b[1->f]) (2)
z[t] = tanh(W[x->c]x[t] + W[h->c]h[t−1] + b[1->c]) (3)
c[t] = f[t]c[t−1] + i[t]z[t] (4)
o[t] = σ(W[x->o]x[t] + W[h->o]h[t−1] + b[1->o]) (5)
h[t] = o[t]tanh(c[t]) (6)i.e. omitting the summands W[c->i]c[t−1] (eq. 1), W[c->f]c[t−1] (eq. 2), and W[c->o]c[t] (eq. 5).
This is a static attribute of the FastLSTM class. The default value is false.
Setting usenngraph = true will force all new instantiated instances of FastLSTM
to use nngraph's nn.gModule to build the internal recurrentModule which is
cloned for each time-step.
This extends the FastLSTM class to enable faster convergence during training by zero-centering the input-to-hidden and hidden-to-hidden transformations.
It reduces the internal covariate shift between time steps. It is an implementation of Cooijmans et. al.'s Recurrent Batch Normalization. The hidden-to-hidden transition of each LSTM cell is normalized according to
i[t] = σ(BN(W[x->i]x[t]) + BN(W[h->i]h[t−1]) + b[1->i]) (1)
f[t] = σ(BN(W[x->f]x[t]) + BN(W[h->f]h[t−1]) + b[1->f]) (2)
z[t] = tanh(BN(W[x->c]x[t]) + BN(W[h->c]h[t−1]) + b[1->c]) (3)
c[t] = f[t]c[t−1] + i[t]z[t] (4)
o[t] = σ(BN(W[x->o]x[t]) + BN(W[h->o]h[t−1]) + b[1->o]) (5)
h[t] = o[t]tanh(c[t]) (6)where the batch normalizing transform is:
BN(h; gamma, beta) = beta + gamma * hd - E(hd)
------------------
sqrt(E(σ(hd) + eps)) where hd is a vector of (pre)activations to be normalized, gamma, and beta are model parameters that determine the mean and standard deviation of the normalized activation. eps is a regularization hyperparameter to keep the division numerically stable and E(hd) and E(σ(hd)) are the estimates of the mean and variance in the mini-batch respectively. The authors recommend initializing gamma to a small value and found 0.1 to be the value that did not cause vanishing gradients. beta, the shift parameter, is null by default.
To turn on batch normalization during training, do:
nn.FastLSTM.bn = true
lstm = nn.FastLSTM(inputsize, outputsize, [rho, eps, momentum, affine]where momentum is same as gamma in the equation above (defaults to 0.1), eps is defined above and affine is a boolean whose state determines if the learnable affine transform is turned off (false) or on (true, the default).
References :
- A. Learning Phrase Representations Using RNN Encoder-Decoder For Statistical Machine Translation.
- B. Implementing a GRU/LSTM RNN with Python and Theano
- C. An Empirical Exploration of Recurrent Network Architectures
- D. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling
- E. RnnDrop: A Novel Dropout for RNNs in ASR
- F. A Theoretically Grounded Application of Dropout in Recurrent Neural Networks
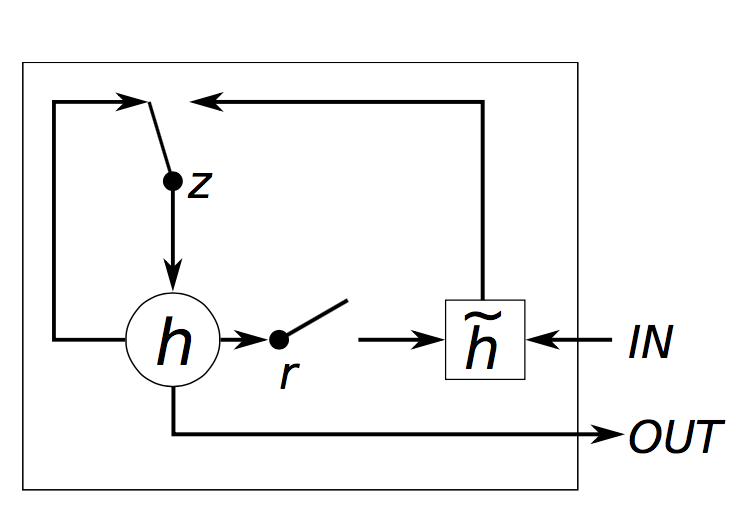
This is an implementation of Gated Recurrent Units module.
The nn.GRU(inputSize, outputSize [,rho [,p [, mono]]]) constructor takes 3 arguments likewise nn.LSTM or 4 arguments for dropout:
inputSize: a number specifying the size of the input;outputSize: a number specifying the size of the output;rho: the maximum amount of backpropagation steps to take back in time. Limits the number of previous steps kept in memory. Defaults to 9999;p: dropout probability for inner connections of GRUs.mono: Monotonic sample for dropouts inside GRUs. Only needed in aTrimZero+BGRU(p>0) situation.
The actual implementation corresponds to the following algorithm:
z[t] = σ(W[x->z]x[t] + W[s->z]s[t−1] + b[1->z]) (1)
r[t] = σ(W[x->r]x[t] + W[s->r]s[t−1] + b[1->r]) (2)
h[t] = tanh(W[x->h]x[t] + W[hr->c](s[t−1]r[t]) + b[1->h]) (3)
s[t] = (1-z[t])h[t] + z[t]s[t-1] (4)where W[s->q] is the weight matrix from s to q, t indexes the time-step, b[1->q] are the biases leading into q, σ() is Sigmoid, x[t] is the input and s[t] is the output of the module (eq. 4). Note that unlike the LSTM, the GRU has no cells.
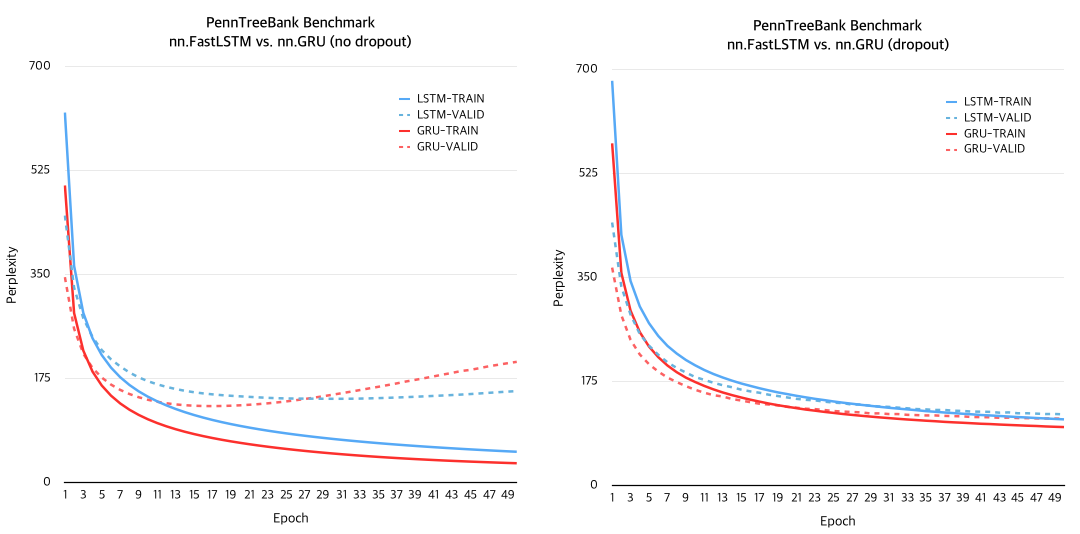
The GRU was benchmark on PennTreeBank dataset using recurrent-language-model.lua script.
It slightly outperfomed FastLSTM, however, since LSTMs have more parameters than GRUs,
the dataset larger than PennTreeBank might change the performance result.
Don't be too hasty to judge on which one is the better of the two (see Ref. C and D).
Memory examples/s
FastLSTM 176M 16.5K
GRU 92M 15.8K
Memory is measured by the size of dp.Experiment save file. examples/s is measured by the training speed at 1 epoch, so, it may have a disk IO bias.
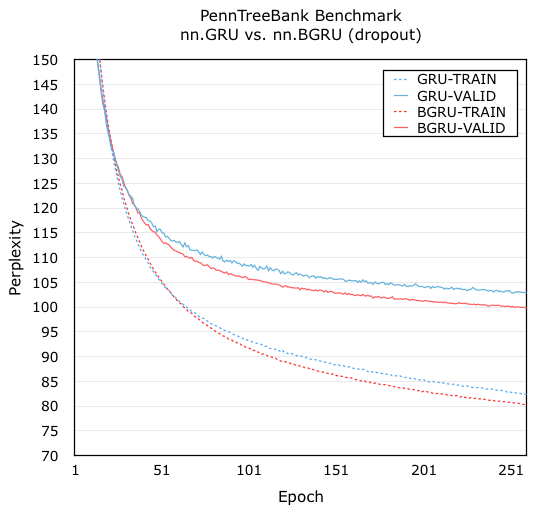
RNN dropout (see Ref. E and F) was benchmark on PennTreeBank dataset using recurrent-language-model.lua script, too. The details can be found in the script. In the benchmark, GRU utilizes a dropout after LookupTable, while BGRU, stands for Bayesian GRUs, uses dropouts on inner connections (naming as Ref. F), but not after LookupTable.
As Yarin Gal (Ref. F) mentioned, it is recommended that one may use p = 0.25 for the first attempt.
To implement GRU, a simple module is added, which cannot be possible to build only using nn modules.
module = nn.SAdd(addend, negate)Applies a single scalar addition to the incoming data, i.e. y_i = x_i + b, then negate all components if negate is true. Which is used to implement s[t] = (1-z[t])h[t] + z[t]s[t-1] of GRU (see above Equation (4)).
nn.SAdd(-1, true)Here, if the incoming data is z[t], then the output becomes -(z[t]-1)=1-z[t]. Notice that nn.Mul() multiplies a scalar which is a learnable parameter.
References :
- A. MuFuRU: The Multi-Function Recurrent Unit.
- B. Tensorflow Implementation of the Multi-Function Recurrent Unit
This is an implementation of the Multi-Function Recurrent Unit module.
The nn.MuFuRu(inputSize, outputSize [,ops [,rho]]) constructor takes 2 required arguments, plus optional arguments:
inputSize: a number specifying the dimension of the input;outputSize: a number specifying the dimension of the output;ops: a table of strings, representing which composition operations should be used. The table can be any subset of{'keep', 'replace', 'mul', 'diff', 'forget', 'sqrt_diff', 'max', 'min'}. By default, all composition operations are enabled.rho: the maximum amount of backpropagation steps to take back in time. Limits the number of previous steps kept in memory. Defaults to 9999;
The Multi-Function Recurrent Unit generalizes the GRU by allowing weightings of arbitrary composition operators to be learned. As in the GRU, the reset gate is computed based on the current input and previous hidden state, and used to compute a new feature vector:
r[t] = σ(W[x->r]x[t] + W[s->r]s[t−1] + b[1->r]) (1)
v[t] = tanh(W[x->v]x[t] + W[sr->v](s[t−1]r[t]) + b[1->v]) (2)where W[a->b] denotes the weight matrix from activation a to b, t denotes the time step, b[1->a] is the bias for activation a, and s[t-1]r[t] is the element-wise multiplication of the two vectors.
Unlike in the GRU, rather than computing a single update gate (z[t] in GRU), MuFuRU computes a weighting over an arbitrary number of composition operators.
A composition operator is any differentiable operator which takes two vectors of the same size, the previous hidden state, and a new feature vector, and returns a new vector representing the new hidden state. The GRU implicitly defines two such operations, keep and replace, defined as keep(s[t-1], v[t]) = s[t-1] and replace(s[t-1], v[t]) = v[t].
Ref. A proposes 6 additional operators, which all operate element-wise:
mul(x,y) = x * ydiff(x,y) = x - yforget(x,y) = 0sqrt_diff(x,y) = 0.25 * sqrt(|x - y|)max(x,y)min(x,y)
The weightings of each operation are computed via a softmax from the current input and previous hidden state, similar to the update gate in the GRU. The produced hidden state is then the element-wise weighted sum of the output of each operation.
p^[t][j] = W[x->pj]x[t] + W[s->pj]s[t−1] + b[1->pj]) (3)
(p[t][1], ... p[t][J]) = softmax (p^[t][1], ..., p^[t][J]) (4)
s[t] = sum(p[t][j] * op[j](s[t-1], v[t])) (5)where p[t][j] is the weightings for operation j at time step t, and sum in equation 5 is over all operators J.
This module decorates a module to be used within an AbstractSequencer instance.
It does this by making the decorated module conform to the AbstractRecurrent interface,
which like the LSTM and Recurrent classes, this class inherits.
rec = nn.Recursor(module[, rho])For each successive call to updateOutput (i.e. forward), this
decorator will create a stepClone() of the decorated module.
So for each time-step, it clones the module. Both the clone and
original share parameters and gradients w.r.t. parameters. However, for
modules that already conform to the AbstractRecurrent interface,
the clone and original module are one and the same (i.e. no clone).
Examples :
Let's assume I want to stack two LSTMs. I could use two sequencers :
lstm = nn.Sequential()
:add(nn.Sequencer(nn.LSTM(100,100)))
:add(nn.Sequencer(nn.LSTM(100,100)))Using a Recursor, I make the same model with a single Sequencer :
lstm = nn.Sequencer(
nn.Recursor(
nn.Sequential()
:add(nn.LSTM(100,100))
:add(nn.LSTM(100,100))
)
)Actually, the Sequencer will wrap any non-AbstractRecurrent module automatically,
so I could simplify this further to :
lstm = nn.Sequencer(
nn.Sequential()
:add(nn.LSTM(100,100))
:add(nn.LSTM(100,100))
)I can also add a Linear between the two LSTMs. In this case,
a Linear will be cloned (and have its parameters shared) for each time-step,
while the LSTMs will do whatever cloning internally :
lstm = nn.Sequencer(
nn.Sequential()
:add(nn.LSTM(100,100))
:add(nn.Linear(100,100))
:add(nn.LSTM(100,100))
)AbstractRecurrent instances like Recursor, Recurrent and LSTM are
expcted to manage time-steps internally. Non-AbstractRecurrent instances
can be wrapped by a Recursor to have the same behavior.
Every call to forward on an AbstractRecurrent instance like Recursor
will increment the self.step attribute by 1, using a shared parameter clone
for each successive time-step (for a maximum of rho time-steps, which defaults to 9999999).
In this way, backward can be called in reverse order of the forward calls
to perform backpropagation through time (BPTT). Which is exactly what
AbstractSequencer instances do internally.
The backward call, which is actually divided into calls to updateGradInput and
accGradParameters, decrements by 1 the self.udpateGradInputStep and self.accGradParametersStep
respectively, starting at self.step.
Successive calls to backward will decrement these counters and use them to
backpropagate through the appropriate internall step-wise shared-parameter clones.
Anyway, in most cases, you will not have to deal with the Recursor object directly as
AbstractSequencer instances automatically decorate non-AbstractRecurrent instances
with a Recursor in their constructors.
For a concrete example of its use, please consult the simple-recurrent-network.lua training script for an example of its use.
A extremely general container for implementing pretty much any type of recurrence.
rnn = nn.Recurrence(recurrentModule, outputSize, nInputDim, [rho])Unlike Recurrent, this module doesn't manage a separate
modules like inputModule, startModule, mergeModule and the like.
Instead, it only manages a single recurrentModule, which should
output a Tensor or table : output(t)
given an input table : {input(t), output(t-1)}.
Using a mix of Recursor (say, via Sequencer) with Recurrence, one can implement
pretty much any type of recurrent neural network, including LSTMs and RNNs.
For the first step, the Recurrence forwards a Tensor (or table thereof)
of zeros through the recurrent layer (like LSTM, unlike Recurrent).
So it needs to know the outputSize, which is either a number or
torch.LongStorage, or table thereof. The batch dimension should be
excluded from the outputSize. Instead, the size of the batch dimension
(i.e. number of samples) will be extrapolated from the input using
the nInputDim argument. For example, say that our input is a Tensor of size
4 x 3 where 4 is the number of samples, then nInputDim should be 1.
As another example, if our input is a table of table [...] of tensors
where the first tensor (depth first) is the same as in the previous example,
then our nInputDim is also 1.
As an example, let's use Sequencer and Recurrence
to build a Simple RNN for language modeling :
rho = 5
hiddenSize = 10
outputSize = 5 -- num classes
nIndex = 10000
-- recurrent module
rm = nn.Sequential()
:add(nn.ParallelTable()
:add(nn.LookupTable(nIndex, hiddenSize))
:add(nn.Linear(hiddenSize, hiddenSize)))
:add(nn.CAddTable())
:add(nn.Sigmoid())
rnn = nn.Sequencer(
nn.Sequential()
:add(nn.Recurrence(rm, hiddenSize, 1))
:add(nn.Linear(hiddenSize, outputSize))
:add(nn.LogSoftMax())
)Note : We could very well reimplement the LSTM module using the
newer Recursor and Recurrent modules, but that would mean
breaking backwards compatibility for existing models saved on disk.
Ref. A : Regularizing RNNs by Stabilizing Activations
This module implements the norm-stabilization criterion:
ns = nn.NormStabilizer([beta])This module regularizes the hidden states of RNNs by minimizing the difference between the L2-norms of consecutive steps. The cost function is defined as :
loss = beta * 1/T sum_t( ||h[t]|| - ||h[t-1]|| )^2
where T is the number of time-steps. Note that we do not divide the gradient by T
such that the chosen beta can scale to different sequence sizes without being changed.
The sole argument beta is defined in ref. A. Since we don't divide the gradients by
the number of time-steps, the default value of beta=1 should be valid for most cases.
This module should be added between RNNs (or LSTMs or GRUs) to provide better regularization of the hidden states. For example :
local stepmodule = nn.Sequential()
:add(nn.FastLSTM(10,10))
:add(nn.NormStabilizer())
:add(nn.FastLSTM(10,10))
:add(nn.NormStabilizer())
local rnn = nn.Sequencer(stepmodule)To use it with SeqLSTM you can do something like this :
local rnn = nn.Sequential()
:add(nn.SeqLSTM(10,10))
:add(nn.Sequencer(nn.NormStabilizer()))
:add(nn.SeqLSTM(10,10))
:add(nn.Sequencer(nn.NormStabilizer()))This abstract class implements a light interface shared by
subclasses like : Sequencer, Repeater, RecurrentAttention, BiSequencer and so on.
The nn.Sequencer(module) constructor takes a single argument, module, which is the module
to be applied from left to right, on each element of the input sequence.
seq = nn.Sequencer(module)This Module is a kind of decorator
used to abstract away the intricacies of AbstractRecurrent modules. While an AbstractRecurrent instance
requires that a sequence to be presented one input at a time, each with its own call to forward (and backward),
the Sequencer forwards an input sequence (a table) into an output sequence (a table of the same length).
It also takes care of calling forget on AbstractRecurrent instances.
The Sequencer requires inputs and outputs to be of shape seqlen x batchsize x featsize :
seqlenis the number of time-steps that will be fed into theSequencer.batchsizeis the number of examples in the batch. Each example is its own independent sequence.featsizeis the size of the remaining non-batch dimensions. So this could be1for language models, orc x h x wfor convolutional models, etc.
Above is an example input sequence for a character level language model.
It has seqlen is 5 which means that it contains sequences of 5 time-steps.
The openning { and closing } illustrate that the time-steps are elements of a Lua table, although
it also accepts full Tensors of shape seqlen x batchsize x featsize.
The batchsize is 2 as their are two independent sequences : { H, E, L, L, O } and { F, U, Z, Z, Y, }.
The featsize is 1 as their is only one feature dimension per character and each such character is of size 1.
So the input in this case is a table of seqlen time-steps where each time-step is represented by a batchsize x featsize Tensor.
Above is another example of a sequence (input or output).
It has a seqlen of 4 time-steps.
The batchsize is again 2 which means there are two sequences.
The featsize is 3 as each time-step of each sequence has 3 variables.
So each time-step (element of the table) is represented again as a tensor
of size batchsize x featsize.
Note that while in both examples the featsize encodes one dimension,
it could encode more.
For example, rnn : an instance of nn.AbstractRecurrent, can forward an input sequence one forward at a time:
input = {torch.randn(3,4), torch.randn(3,4), torch.randn(3,4)}
rnn:forward(input[1])
rnn:forward(input[2])
rnn:forward(input[3])Equivalently, we can use a Sequencer to forward the entire input sequence at once:
seq = nn.Sequencer(rnn)
seq:forward(input)We can also forward Tensors instead of Tables :
-- seqlen x batchsize x featsize
input = torch.randn(3,3,4)
seq:forward(input)The Sequencer can also take non-recurrent Modules (i.e. non-AbstractRecurrent instances) and apply it to each
input to produce an output table of the same length.
This is especially useful for processing variable length sequences (tables).
Internally, the Sequencer expects the decorated module to be an
AbstractRecurrent instance. When this is not the case, the module
is automatically decorated with a Recursor module, which makes it
conform to the AbstractRecurrent interface.
Note : this is due a recent update (27 Oct 2015), as before this
AbstractRecurrent and and non-AbstractRecurrent instances needed to
be decorated by their own Sequencer. The recent update, which introduced the
Recursor decorator, allows a single Sequencer to wrap any type of module,
AbstractRecurrent, non-AbstractRecurrent or a composite structure of both types.
Nevertheless, existing code shouldn't be affected by the change.
For a concise example of its use, please consult the simple-sequencer-network.lua training script.
When mode='neither' (the default behavior of the class), the Sequencer will additionally call forget before each call to forward.
When mode='both' (the default when calling this function), the Sequencer will never call forget.
In which case, it is up to the user to call forget between independent sequences.
This behavior is only applicable to decorated AbstractRecurrent modules.
Accepted values for argument mode are as follows :
- 'eval' only affects evaluation (recommended for RNNs)
- 'train' only affects training
- 'neither' affects neither training nor evaluation (default behavior of the class)
- 'both' affects both training and evaluation (recommended for LSTMs)
Calls the decorated AbstractRecurrent module's forget method.
This module is a faster version of nn.Sequencer(nn.FastLSTM(inputsize, outputsize)) :
seqlstm = nn.SeqLSTM(inputsize, outputsize)Each time-step is computed as follows (same as FastLSTM):
i[t] = σ(W[x->i]x[t] + W[h->i]h[t−1] + b[1->i]) (1)
f[t] = σ(W[x->f]x[t] + W[h->f]h[t−1] + b[1->f]) (2)
z[t] = tanh(W[x->c]x[t] + W[h->c]h[t−1] + b[1->c]) (3)
c[t] = f[t]c[t−1] + i[t]z[t] (4)
o[t] = σ(W[x->o]x[t] + W[h->o]h[t−1] + b[1->o]) (5)
h[t] = o[t]tanh(c[t]) (6)A notable difference is that this module expects the input and gradOutput to
be tensors instead of tables. The default shape is seqlen x batchsize x inputsize for
the input and seqlen x batchsize x outputsize for the output :
input = torch.randn(seqlen, batchsize, inputsize)
gradOutput = torch.randn(seqlen, batchsize, outputsize)
output = seqlstm:forward(input)
gradInput = seqlstm:backward(input, gradOutput)Note that if you prefer to transpose the first two dimension (i.e. batchsize x seqlen instead of the default seqlen x batchsize)
you can set seqlstm.batchfirst = true following initialization.
For variable length sequences, set seqlstm.maskzero = true.
This is equivalent to calling maskZero(1) on a FastLSTM wrapped by a Sequencer:
fastlstm = nn.FastLSTM(inputsize, outputsize)
fastlstm:maskZero(1)
seqfastlstm = nn.Sequencer(fastlstm)For maskzero = true, input sequences are expected to be seperated by tensor of zeros for a time step.
The seqlstm:toFastLSTM() method generates a FastLSTM instance initialized with the parameters
of the seqlstm instance. Note however that the resulting parameters will not be shared (nor can they ever be).
Like the FastLSTM, the SeqLSTM does not use peephole connections between cell and gates (see FastLSTM for details).
Like the Sequencer, the SeqLSTM provides a remember method.
Note that a SeqLSTM cannot replace FastLSTM in code that decorates it with a
AbstractSequencer or Recursor as this would be equivalent to Sequencer(Sequencer(FastLSTM)).
You have been warned.
References:
- A. LSTM RNN Architectures for Large Scale Acoustic Modeling
- B. Exploring the Limits of Language Modeling
lstmp = nn.SeqLSTMP(inputsize, hiddensize, outputsize)The SeqLSTMP is a subclass of SeqLSTM.
It differs in that after computing the hidden state h[t] (eq. 6), it is
projected onto r[t] using a simple linear transform (eq. 7).
The computation of the gates also uses the previous such projection r[t-1] (eq. 1, 2, 3, 5).
This differs from SeqLSTM which uses h[t-1] instead of r[t-1].
The computation of a time-step outlined in SeqLSTM is replaced with the following:
i[t] = σ(W[x->i]x[t] + W[r->i]r[t−1] + b[1->i]) (1)
f[t] = σ(W[x->f]x[t] + W[r->f]r[t−1] + b[1->f]) (2)
z[t] = tanh(W[x->c]x[t] + W[h->c]r[t−1] + b[1->c]) (3)
c[t] = f[t]c[t−1] + i[t]z[t] (4)
o[t] = σ(W[x->o]x[t] + W[r->o]r[t−1] + b[1->o]) (5)
h[t] = o[t]tanh(c[t]) (6)
r[t] = W[h->r]h[t] (7)The algorithm is outlined in ref. A and benchmarked with state of the art results on the Google billion words dataset in ref. B.
SeqLSTMP can be used with an hiddensize >> outputsize such that the effective size of the memory cells c[t]
and gates i[t], f[t] and o[t] can be much larger than the actual input x[t] and output r[t].
For fixed inputsize and outputsize, the SeqLSTMP will be able to remember much more information than the SeqLSTM.
This module is a faster version of nn.Sequencer(nn.GRU(inputsize, outputsize)) :
seqGRU = nn.SeqGRU(inputsize, outputsize)Usage of SeqGRU differs from GRU in the same manner as SeqLSTM differs from LSTM. Therefore see SeqLSTM for more details.
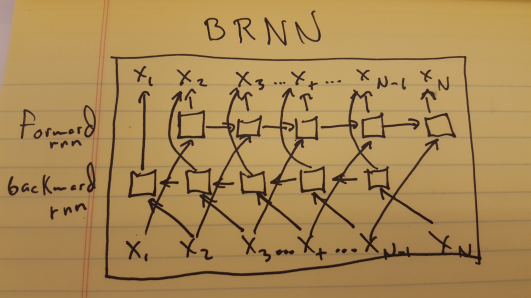
brnn = nn.SeqBRNN(inputSize, outputSize, [batchFirst], [merge])A bi-directional RNN that uses SeqLSTM. Internally contains a 'fwd' and 'bwd' module of SeqLSTM. Expects an input shape of seqlen x batchsize x inputsize.
By setting [batchFirst] to true, the input shape can be batchsize x seqLen x inputsize. Merge module defaults to CAddTable(), summing the outputs from each
output layer.
Example:
input = torch.rand(1, 1, 5)
brnn = nn.SeqBRNN(5, 5)
print(brnn:forward(input))
Prints an output of a 1x1x5 tensor.
Applies encapsulated fwd and bwd rnns to an input sequence in forward and reverse order.
It is used for implementing Bidirectional RNNs and LSTMs.
brnn = nn.BiSequencer(fwd, [bwd, merge])The input to the module is a sequence (a table) of tensors
and the output is a sequence (a table) of tensors of the same length.
Applies a fwd rnn (an AbstractRecurrent instance) to each element in the sequence in
forward order and applies the bwd rnn in reverse order (from last element to first element).
The bwd rnn defaults to:
bwd = fwd:clone()
bwd:reset()For each step (in the original sequence), the outputs of both rnns are merged together using
the merge module (defaults to nn.JoinTable(1,1)).
If merge is a number, it specifies the JoinTable
constructor's nInputDim argument. Such that the merge module is then initialized as :
merge = nn.JoinTable(1,merge)Internally, the BiSequencer is implemented by decorating a structure of modules that makes
use of 3 Sequencers for the forward, backward and merge modules.
Similarly to a Sequencer, the sequences in a batch must have the same size. But the sequence length of each batch can vary.
Note : make sure you call brnn:forget() after each call to updateParameters().
Alternatively, one could call brnn.bwdSeq:forget() so that only bwd rnn forgets.
This is the minimum requirement, as it would not make sense for the bwd rnn to remember future sequences.
Applies encapsulated fwd and bwd rnns to an input sequence in forward and reverse order.
It is used for implementing Bidirectional RNNs and LSTMs for Language Models (LM).
brnn = nn.BiSequencerLM(fwd, [bwd, merge])The input to the module is a sequence (a table) of tensors
and the output is a sequence (a table) of tensors of the same length.
Applies a fwd rnn (an AbstractRecurrent instance to the
first N-1 elements in the sequence in forward order.
Applies the bwd rnn in reverse order to the last N-1 elements (from second-to-last element to first element).
This is the main difference of this module with the BiSequencer.
The latter cannot be used for language modeling because the bwd rnn would be trained to predict the input it had just be fed as input.
The bwd rnn defaults to:
bwd = fwd:clone()
bwd:reset()While the fwd rnn will output representations for the last N-1 steps,
the bwd rnn will output representations for the first N-1 steps.
The missing outputs for each rnn ( the first step for the fwd, the last step for the bwd)
will be filled with zero Tensors of the same size the commensure rnn's outputs.
This way they can be merged. If nn.JoinTable is used (the default), then the first
and last output elements will be padded with zeros for the missing fwd and bwd rnn outputs, respectively.
For each step (in the original sequence), the outputs of both rnns are merged together using
the merge module (defaults to nn.JoinTable(1,1)).
If merge is a number, it specifies the JoinTable
constructor's nInputDim argument. Such that the merge module is then initialized as :
merge = nn.JoinTable(1,merge)Similarly to a Sequencer, the sequences in a batch must have the same size. But the sequence length of each batch can vary.
Note that LMs implemented with this module will not be classical LMs as they won't measure the probability of a word given the previous words. Instead, they measure the probabiliy of a word given the surrounding words, i.e. context. While for mathematical reasons you may not be able to use this to measure the probability of a sequence of words (like a sentence), you can still measure the pseudo-likeliness of such a sequence (see this for a discussion).
This Module is a decorator similar to Sequencer.
It differs in that the sequence length is fixed before hand and the input is repeatedly forwarded
through the wrapped module to produce an output table of length nStep:
r = nn.Repeater(module, nStep)Argument module should be an AbstractRecurrent instance.
This is useful for implementing models like RCNNs,
which are repeatedly presented with the same input.
References :
- A. Recurrent Models of Visual Attention
- B. Simple Statistical Gradient-Following Algorithms for Connectionist Reinforcement Learning
This module can be used to implement the Recurrent Attention Model (RAM) presented in Ref. A :
ram = nn.RecurrentAttention(rnn, action, nStep, hiddenSize)rnn is an AbstractRecurrent instance.
Its input is {x, z} where x is the input to the ram and z is an
action sampled from the action module.
The output size of the rnn must be equal to hiddenSize.
action is a Module
that uses a REINFORCE module (ref. B) like
ReinforceNormal,
ReinforceCategorical, or
ReinforceBernoulli
to sample actions given the previous time-step's output of the rnn.
During the first time-step, the action module is fed with a Tensor of zeros of size input:size(1) x hiddenSize.
It is important to understand that the sampled actions do not receive gradients
backpropagated from the training criterion.
Instead, a reward is broadcast from a Reward Criterion like VRClassReward Criterion to
the action's REINFORCE module, which will backprogate graidents computed from the output samples
and the reward.
Therefore, the action module's outputs are only used internally, within the RecurrentAttention module.
nStep is the number of actions to sample, i.e. the number of elements in the output table.
hiddenSize is the output size of the rnn. This variable is necessary
to generate the zero Tensor to sample an action for the first step (see above).
A complete implementation of Ref. A is available here.
This module zeroes the output rows of the decorated module
for commensurate input rows which are tensors of zeros.
mz = nn.MaskZero(module, nInputDim)The output Tensor (or table thereof) of the decorated module
will have each row (samples) zeroed when the commensurate row of the input
is a tensor of zeros.
The nInputDim argument must specify the number of non-batch dims
in the first Tensor of the input. In the case of an input table,
the first Tensor is the first one encountered when doing a depth-first search.
This decorator makes it possible to pad sequences with different lengths in the same batch with zero vectors.
Caveat: MaskZero not guarantee that the output and gradInput tensors of the internal modules
of the decorated module will be zeroed as well when the input is zero as well.
MaskZero only affects the immediate gradInput and output of the module that it encapsulates.
However, for most modules, the gradient update for that time-step will be zero because
backpropagating a gradient of zeros will typically yield zeros all the way to the input.
In this respect, modules to avoid in encapsulating inside a MaskZero are AbsractRecurrent
instances as the flow of gradients between different time-steps internally.
Instead, call the AbstractRecurrent.maskZero method
to encapsulate the internal recurrentModule.
WARNING : only use this module if your input contains lots of zeros.
In almost all cases, MaskZero will be faster, especially with CUDA.
Ref. A : TrimZero: A Torch Recurrent Module for Efficient Natural Language Processing
The usage is the same with MaskZero.
mz = nn.TrimZero(module, nInputDim)The only difference from MaskZero is that it reduces computational costs by varying a batch size, if any, for the case that varying lengths are provided in the input.
Notice that when the lengths are consistent, MaskZero will be faster, because TrimZero has an operational cost.
In short, the result is the same with MaskZero's, however, TrimZero is faster than MaskZero only when sentence lengths is costly vary.
In practice, e.g. language model, TrimZero is expected to be faster than MaskZero about 30%. (You can test with it using test/test_trimzero.lua.)
This module extends nn.LookupTable to support zero indexes. Zero indexes are forwarded as zero tensors.
lt = nn.LookupTableMaskZero(nIndex, nOutput)The output Tensor will have each row zeroed when the commensurate row of the input is a zero index.
This lookup table makes it possible to pad sequences with different lengths in the same batch with zero vectors.
This criterion zeroes the err and gradInput rows of the decorated criterion
for commensurate input rows which are tensors of zeros.
mzc = nn.MaskZeroCriterion(criterion, nInputDim)The gradInput Tensor (or table thereof) of the decorated criterion
will have each row (samples) zeroed when the commensurate row of the input
is a tensor of zeros. The err will also disregard such zero rows.
The nInputDim argument must specify the number of non-batch dims
in the first Tensor of the input. In the case of an input table,
the first Tensor is the first one encountered when doing a depth-first search.
This decorator makes it possible to pad sequences with different lengths in the same batch with zero vectors.
reverseSeq = nn.SeqReverseSequence(dim)Reverses an input tensor on a specified dimension. The reversal dimension can be no larger than three.
Example:
input = torch.Tensor({{1,2,3,4,5}, {6,7,8,9,10}})
reverseSeq = nn.SeqReverseSequence(1)
print(reverseSeq:forward(input))
Gives us an output of torch.Tensor({{6,7,8,9,10},{1,2,3,4,5}})
This Criterion is a decorator:
c = nn.SequencerCriterion(criterion, [sizeAverage])Both the input and target are expected to be a sequence, either as a table or Tensor.
For each step in the sequence, the corresponding elements of the input and target
will be applied to the criterion.
The output of forward is the sum of all individual losses in the sequence.
This is useful when used in conjunction with a Sequencer.
If sizeAverage is true (default is false), the output loss and gradInput is averaged over each time-step.
This Criterion is a decorator:
c = nn.RepeaterCriterion(criterion)The input is expected to be a sequence (table or Tensor). A single target is
repeatedly applied using the same criterion to each element in the input sequence.
The output of forward is the sum of all individual losses in the sequence.
This is useful for implementing models like RCNNs,
which are repeatedly presented with the same target.